Ecco le nostre soluzioni al
Sarà mica matematica 20 del prof. Davide
Quesito 1
Per la classe prima hanno risposto correttamente: Bachisio, Gabriele G., Pietro P., Pietro S.
Pierluigi e qualcun altro invece non sono stati precisi, hanno parlato di somma dei numeri delle pagine e non di somma delle cifre dei numeri di pagina.
Per la classe terza rispondono: Davì, Beatrice, Davide D. e Marco D.
La soluzione data è sostanzialmente la seguente [prendo il meglio dagli uni e dagli altri. I ragazzi di prima affermano quasi tutti: ho preso anche io un libro e l'ho aperto in una pagina qualsiasi. Ho subito visto che ... ]:
Il professore non accetta, perché sommando le cifre dei numeri delle due pagine si ottiene sempre un numero dispari e vengono interrogati solo gli alunni che corrispondono al numero dispari nell’elenco. Questo perché: a sinistra la pagina è sempre pari, la somma delle cifre può essere sia pari e allora la somma delle cifre a destra sarà dispari, sia dispari e allora la somma delle cifre a destra sarà pari, perché la pagina a destra ha una unità in più. E quindi: P+D e D+P è sempre uguale a D.
Quesito 2
Questo si è rivelato più ostico per i ragazzi della prima: quasi tutti coloro che hanno risolto il primo quesito, a cui si aggiunge Marco, danno la risposta ma non spiegano correttamente il ragionamento: essi presuppongonomediane due dei segmenti paralleli ai lati del quadrato e quadrati due dei rettangoli di cui si conosce il perimetro. Ancora una volta ripetiamo: in matematica occorre dimostrare quanto si ipotizza, non ci si può affidare solamente a ciò che vedono i nostri occhi.
Gabriele G. spiega invece così:
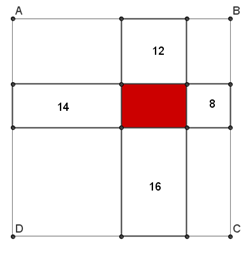
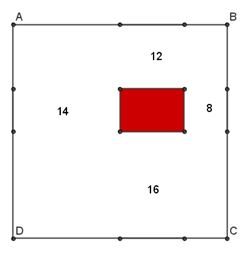
Se spostiamo i lati interni dei rettangoli di cui è indicato il perimetro, sui lati del quadrato ABCD, otteniamo la misura totale di 3 lati di ciascuna delle figure (cioè 40 cm, il perimetro del quadrato). I lati rimasti uno di ogni rettangolo, formano il perimetro del rettangolo rosso.
Siccome conosciamo il perimetro totale delle figure (14 cm+12 cm+8 cm +16 cm=50 cm) possiamo facilmente trovare il perimetro del rettangolo rosso facendo la differenza tra le 2 misure: 50 cm – 40 cm = 10 cm !
Le immagini forse chiariscono meglio:
I ragazzi di terza, ancora Davì, Beatrice, Davide D. e Marco D., che hanno ormai confidenza con il calcolo letterale, lo utilizzano nella soluzione.
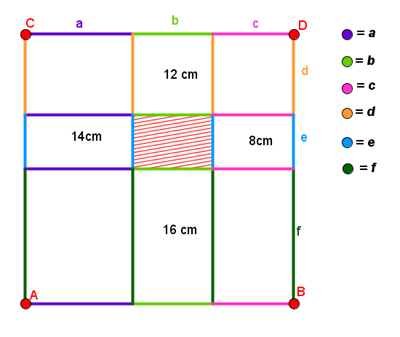
Copio immagine e testo dal geogebra di Beatrice:
(12+14+16+8) cm - Perimetro ABCD =
= (12+14+16+8) cm – 40 cm = 10 cm = Perimetro rettangolo tratteggiato.
DIMOSTRAZIONE
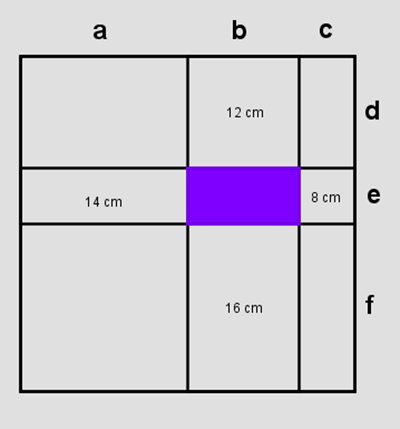
(2a+4b+2c+2d+4e+2f)-(2a+2b+2c+2d+2e+2f)=
= 2a+4b+2c+2d+4e+2f-2a-2b-2c-2d-2e-2f=
= 2b+2e
Le seguenti, dal geogebra di Davì:
Avrebbero potuto lavorare con i semiperimetri ma, tant’è!![]()
Bravi, raga, e,
per dirla con il prof Davide, peccato per chi non ci ha provato![]()